2017-07-23 07:51:42 +00:00
|
|
|
# EWMA [](https://godoc.org/github.com/VividCortex/ewma) 
|
2016-10-31 15:50:02 +00:00
|
|
|
|
|
|
|
|
This repo provides Exponentially Weighted Moving Average algorithms, or EWMAs for short, [based on our
|
|
|
|
|
Quantifying Abnormal Behavior talk](https://vividcortex.com/blog/2013/07/23/a-fast-go-library-for-exponential-moving-averages/).
|
|
|
|
|
|
|
|
|
|
### Exponentially Weighted Moving Average
|
|
|
|
|
|
|
|
|
|
An exponentially weighted moving average is a way to continuously compute a type of
|
|
|
|
|
average for a series of numbers, as the numbers arrive. After a value in the series is
|
|
|
|
|
added to the average, its weight in the average decreases exponentially over time. This
|
|
|
|
|
biases the average towards more recent data. EWMAs are useful for several reasons, chiefly
|
|
|
|
|
their inexpensive computational and memory cost, as well as the fact that they represent
|
|
|
|
|
the recent central tendency of the series of values.
|
|
|
|
|
|
|
|
|
|
The EWMA algorithm requires a decay factor, alpha. The larger the alpha, the more the average
|
|
|
|
|
is biased towards recent history. The alpha must be between 0 and 1, and is typically
|
|
|
|
|
a fairly small number, such as 0.04. We will discuss the choice of alpha later.
|
|
|
|
|
|
|
|
|
|
The algorithm works thus, in pseudocode:
|
|
|
|
|
|
|
|
|
|
1. Multiply the next number in the series by alpha.
|
|
|
|
|
2. Multiply the current value of the average by 1 minus alpha.
|
|
|
|
|
3. Add the result of steps 1 and 2, and store it as the new current value of the average.
|
|
|
|
|
4. Repeat for each number in the series.
|
|
|
|
|
|
|
|
|
|
There are special-case behaviors for how to initialize the current value, and these vary
|
|
|
|
|
between implementations. One approach is to start with the first value in the series;
|
|
|
|
|
another is to average the first 10 or so values in the series using an arithmetic average,
|
|
|
|
|
and then begin the incremental updating of the average. Each method has pros and cons.
|
|
|
|
|
|
|
|
|
|
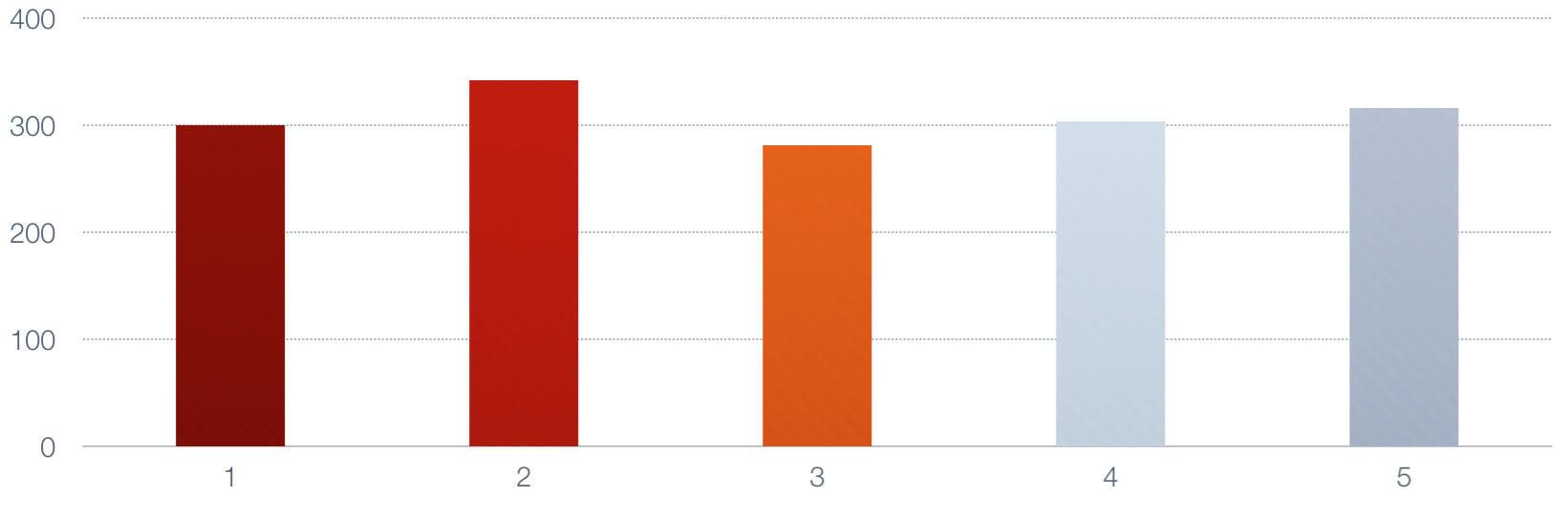
It may help to look at it pictorially. Suppose the series has five numbers, and we choose
|
|
|
|
|
alpha to be 0.50 for simplicity. Here's the series, with numbers in the neighborhood of 300.
|
|
|
|
|
|
2017-07-23 07:51:42 +00:00
|
|
|
|
2016-10-31 15:50:02 +00:00
|
|
|
|
|
|
|
|
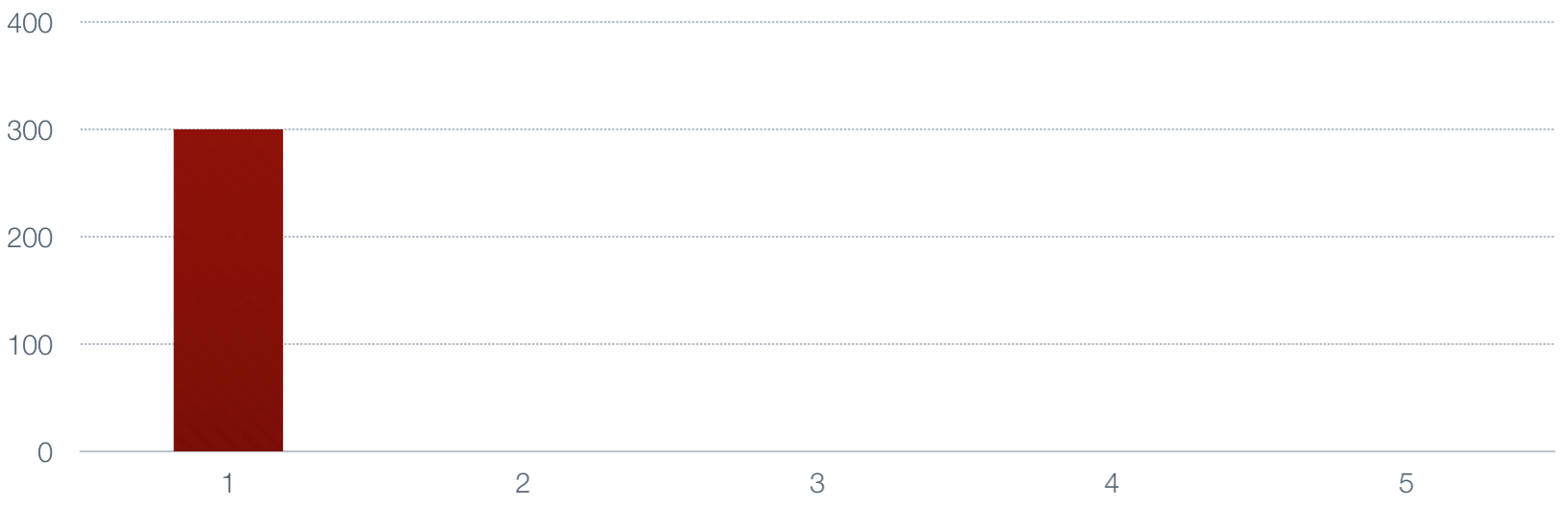
Now let's take the moving average of those numbers. First we set the average to the value
|
|
|
|
|
of the first number.
|
|
|
|
|
|
2017-07-23 07:51:42 +00:00
|
|
|
|
2016-10-31 15:50:02 +00:00
|
|
|
|
|
|
|
|
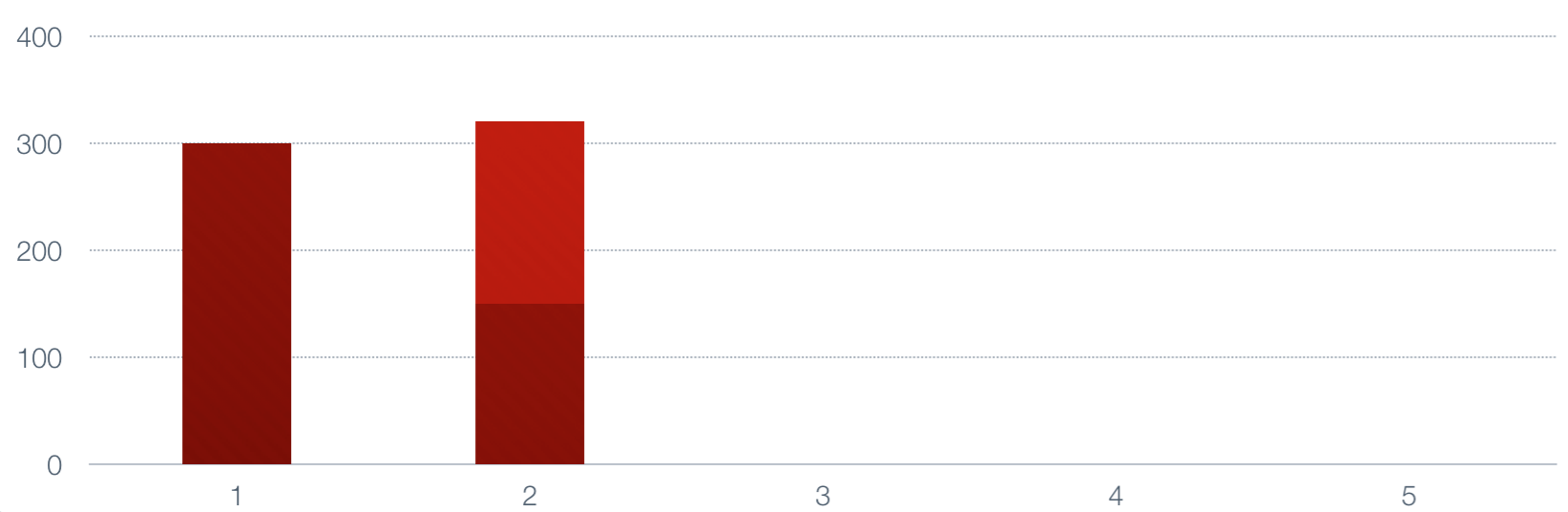
Next we multiply the next number by alpha, multiply the current value by 1-alpha, and add
|
|
|
|
|
them to generate a new value.
|
|
|
|
|
|
2017-07-23 07:51:42 +00:00
|
|
|
|
2016-10-31 15:50:02 +00:00
|
|
|
|
|
|
|
|
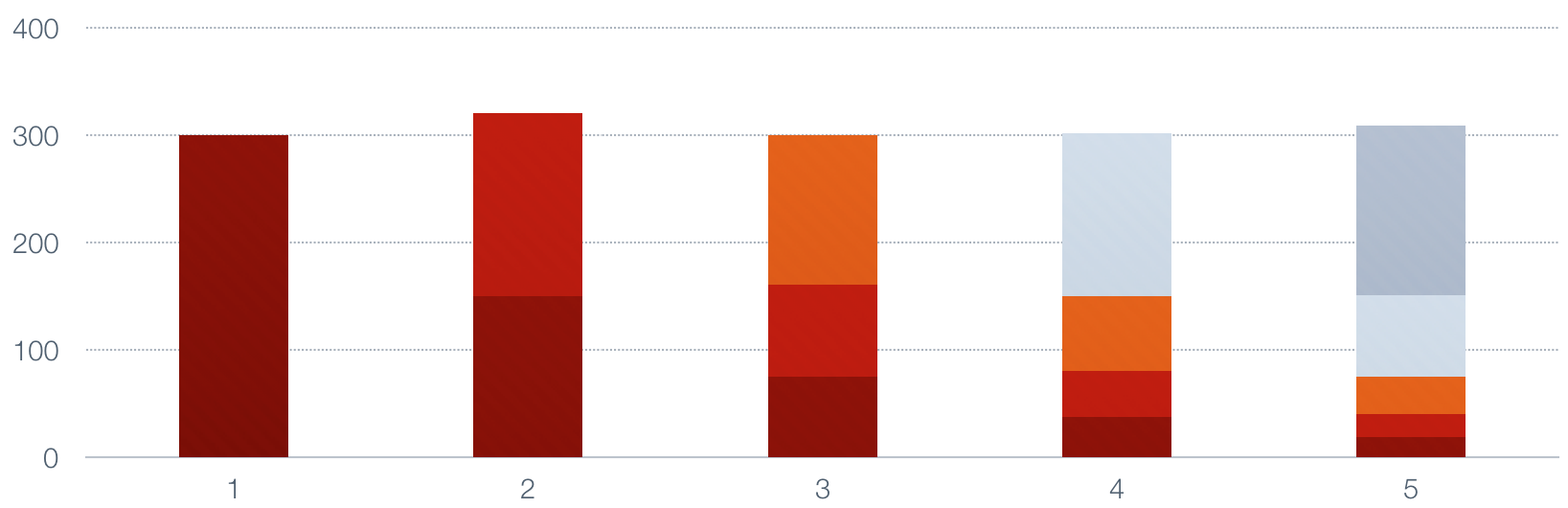
This continues until we are done.
|
|
|
|
|
|
2017-07-23 07:51:42 +00:00
|
|
|
|
2016-10-31 15:50:02 +00:00
|
|
|
|
|
|
|
|
Notice how each of the values in the series decays by half each time a new value
|
|
|
|
|
is added, and the top of the bars in the lower portion of the image represents the
|
|
|
|
|
size of the moving average. It is a smoothed, or low-pass, average of the original
|
|
|
|
|
series.
|
|
|
|
|
|
|
|
|
|
For further reading, see [Exponentially weighted moving average](http://en.wikipedia.org/wiki/Moving_average#Exponential_moving_average) on wikipedia.
|
|
|
|
|
|
|
|
|
|
### Choosing Alpha
|
|
|
|
|
|
|
|
|
|
Consider a fixed-size sliding-window moving average (not an exponentially weighted moving average)
|
|
|
|
|
that averages over the previous N samples. What is the average age of each sample? It is N/2.
|
|
|
|
|
|
|
|
|
|
Now suppose that you wish to construct a EWMA whose samples have the same average age. The formula
|
|
|
|
|
to compute the alpha required for this is: alpha = 2/(N+1). Proof is in the book
|
|
|
|
|
"Production and Operations Analysis" by Steven Nahmias.
|
|
|
|
|
|
|
|
|
|
So, for example, if you have a time-series with samples once per second, and you want to get the
|
|
|
|
|
moving average over the previous minute, you should use an alpha of .032786885. This, by the way,
|
|
|
|
|
is the constant alpha used for this repository's SimpleEWMA.
|
|
|
|
|
|
|
|
|
|
### Implementations
|
|
|
|
|
|
|
|
|
|
This repository contains two implementations of the EWMA algorithm, with different properties.
|
|
|
|
|
|
|
|
|
|
The implementations all conform to the MovingAverage interface, and the constructor returns
|
|
|
|
|
that type.
|
|
|
|
|
|
|
|
|
|
Current implementations assume an implicit time interval of 1.0 between every sample added.
|
|
|
|
|
That is, the passage of time is treated as though it's the same as the arrival of samples.
|
|
|
|
|
If you need time-based decay when samples are not arriving precisely at set intervals, then
|
|
|
|
|
this package will not support your needs at present.
|
|
|
|
|
|
|
|
|
|
#### SimpleEWMA
|
|
|
|
|
|
|
|
|
|
A SimpleEWMA is designed for low CPU and memory consumption. It **will** have different behavior than the VariableEWMA
|
|
|
|
|
for multiple reasons. It has no warm-up period and it uses a constant
|
|
|
|
|
decay. These properties let it use less memory. It will also behave
|
|
|
|
|
differently when it's equal to zero, which is assumed to mean
|
|
|
|
|
uninitialized, so if a value is likely to actually become zero over time,
|
|
|
|
|
then any non-zero value will cause a sharp jump instead of a small change.
|
|
|
|
|
|
|
|
|
|
#### VariableEWMA
|
|
|
|
|
|
|
|
|
|
Unlike SimpleEWMA, this supports a custom age which must be stored, and thus uses more memory.
|
|
|
|
|
It also has a "warmup" time when you start adding values to it. It will report a value of 0.0
|
|
|
|
|
until you have added the required number of samples to it. It uses some memory to store the
|
|
|
|
|
number of samples added to it. As a result it uses a little over twice the memory of SimpleEWMA.
|
|
|
|
|
|
|
|
|
|
## Usage
|
|
|
|
|
|
|
|
|
|
### API Documentation
|
|
|
|
|
|
|
|
|
|
View the GoDoc generated documentation [here](http://godoc.org/github.com/VividCortex/ewma).
|
|
|
|
|
|
|
|
|
|
```go
|
|
|
|
|
package main
|
2017-09-30 14:27:27 +00:00
|
|
|
|
2016-10-31 15:50:02 +00:00
|
|
|
import "github.com/VividCortex/ewma"
|
|
|
|
|
|
|
|
|
|
func main() {
|
2017-09-30 14:27:27 +00:00
|
|
|
samples := [100]float64{
|
|
|
|
|
4599, 5711, 4746, 4621, 5037, 4218, 4925, 4281, 5207, 5203, 5594, 5149,
|
|
|
|
|
}
|
2016-10-31 15:50:02 +00:00
|
|
|
|
2017-09-30 14:27:27 +00:00
|
|
|
e := ewma.NewMovingAverage() //=> Returns a SimpleEWMA if called without params
|
|
|
|
|
a := ewma.NewMovingAverage(5) //=> returns a VariableEWMA with a decay of 2 / (5 + 1)
|
2016-10-31 15:50:02 +00:00
|
|
|
|
2017-09-30 14:27:27 +00:00
|
|
|
for _, f := range samples {
|
|
|
|
|
e.Add(f)
|
|
|
|
|
a.Add(f)
|
|
|
|
|
}
|
2016-10-31 15:50:02 +00:00
|
|
|
|
2017-09-30 14:27:27 +00:00
|
|
|
e.Value() //=> 13.577404704631077
|
|
|
|
|
a.Value() //=> 1.5806140565521463e-12
|
2016-10-31 15:50:02 +00:00
|
|
|
}
|
|
|
|
|
```
|
|
|
|
|
|
|
|
|
|
## Contributing
|
|
|
|
|
|
|
|
|
|
We only accept pull requests for minor fixes or improvements. This includes:
|
|
|
|
|
|
|
|
|
|
* Small bug fixes
|
|
|
|
|
* Typos
|
|
|
|
|
* Documentation or comments
|
|
|
|
|
|
|
|
|
|
Please open issues to discuss new features. Pull requests for new features will be rejected,
|
|
|
|
|
so we recommend forking the repository and making changes in your fork for your use case.
|
|
|
|
|
|
|
|
|
|
## License
|
|
|
|
|
|
|
|
|
|
This repository is Copyright (c) 2013 VividCortex, Inc. All rights reserved.
|
|
|
|
|
It is licensed under the MIT license. Please see the LICENSE file for applicable license terms.
|